Quantum theory is an extraordinarily successful physical theory that underpins our understanding of everything, ranging from the subatomic world to the structure and evolution of stars. But, from the beginnings of its creation in the 1920s, it’s been of great interest for a quite different reason: namely, that it seems to undermine some of the fundamental tenets of the mechanical view of nature that underpinned the development of physics for well over 250 years. So why is that? What exactly is the problem? What is lacking? How is it that we have something that’s so extraordinarily successful and we can use it very well and, at the same time, we say we don’t really understand it. It’s mysterious. It’s obscure. What’s that actually mean? I think a way to get a handle on that is to look at the situation that we have in classical physics which we say that we do understand relatively well.
I think the situation that we have in classical physics is the following. That it has a tripartite structure. We have, at the bottom, a classical conception of reality, this mechanical view, this mathematical conception of how the universe is put together, and when this is mathematized in a very natural way, it leads to the classical mechanical framework.
So this classical conception is this majestic vision of the universe being this great mechanism where everything that exists is matter in motion on the fixed stage of space moving in step with a universal time according to deterministic and reversible universal laws. So it’s this very majestic idea. That’s the ontological part of the statement. There’s also the statement about how we relate to that: in principle, observers have this unfettered access to what’s going on and can do so without disturbing what’s going on.
And the universe is so constituted from this that finite observers, who are necessarily restricted in their ability to probe reality—they have to probe it a piece at a time—they none the less can aspire to put all these little pieces of knowledge together, and aspire to a global understanding of these rules of nature. So the mechanical conception makes great promise and sense to us as finite beings, that we can come to know this whole thing.
When that’s mathematized in a natural way—obviously Newton and Galileo were the first to do this in a big way—this framework is the notion that separation between states and evolution, and laws being deterministic and reversible. And then we build specific theories like Newtonian mechanics, Maxwell’s electrodynamics, thermodynamics, GR, SR, and so on within this basic framework. So, you need to put specific extra input in here to get from here to here. And I think it’s this tripartite structure that gives us the feeling that we understand classical physics. We can span all the way from a conception to specific theories that apply to specific physical domains.
In light of this, what is the situation with quantum physics? In the middle we have a mathematical framework which is the Feynman and Dirac quantum formalism, and certainly we have a way to go from the middle to the top; we have a way to construct specific theories, be that relativistic quantum mechanics or quantum field theory. But what we don’t have, after over 80 years, is a quantum conception of reality, which one would like. This is what I think we lack. Since quantum theory was formulated, a lot of effort has been made to get some understanding of what this may be. I think there are two main directions in which progress has been made.
This quantum framework is written in an abstract mathematical language that our intuition has a hard time to access. That’s a legacy of the process by which it was obtained as a relatively ad hoc modification of classical physics, inspired by mathematical guesswork and inputting some new physical ideas. So this structure here is very difficult to directly comprehend.
One of the approaches has been to try to interpret this formalism. That is to say, take it as a given, and then to try to clothe it in some kind of ontological picture, and this has given rise to the Copenhagen interpretation, the many-worlds interpretation, de Broglie-Bohm interpretation, and many others. These have all been very important, very valuable, and guided the exploration of quantum physics in important ways, but one of the things we’ve learned from this is that it’s possible to clothe the quantum formalism in many different ontological clothing. And they all seem to be okay; they all seem to be consistent within themselves. It’s very difficult to choose between them. And also, those kind of interpretational efforts don’t really cast light on the real origin of the mathematics of quantum theory. Why is quantum theory complex? Why does it use these unitary operators and hermitian operators? None of the interpretations illuminate most of those questions.
Another kind of approach that’s been taken is to try to, as it were, draw out from this formalism general physical properties, which we can get a handle on; the idea is to give us a way to get a conceptual handle on what the mathematics is saying. And so, we have things like the fact that measurements are probabilistic, the idea of complimentarily developed by Niels Bohr, entanglement, these were known within a few years after the quantum formalism was created. Things like no cloning were discovered in the 1980s. Nonlocality, contextuality, much later. So once again the idea here is to extract out something from the quantum formalism that we can get a conceptual grip on. Many more of these properties have been discovered over the last 30 years, which seem to distinguish quantum reality, loosely speaking, from classical reality.
A picture like this, though, raises the question of how do I, in my mind, assemble all of these features into a coherent picture? If these are pieces of a jigsaw, how do I assemble them into a uniform whole? To put it another way, what’s the big idea that lies behind all of these separate ideas? Presumably, some of these are primary, more fundamental, and some are secondary. But which, and how do I know that? This line of development leads to this problem—how do we go from here to a conception of reality?
These difficulties have led, over the last 15-20 years, to a great deal of interest in finding another way to investigate this question about what quantum reality is like.
[Q]: When you’re talking about a classical conception of reality, what do you have in mind?
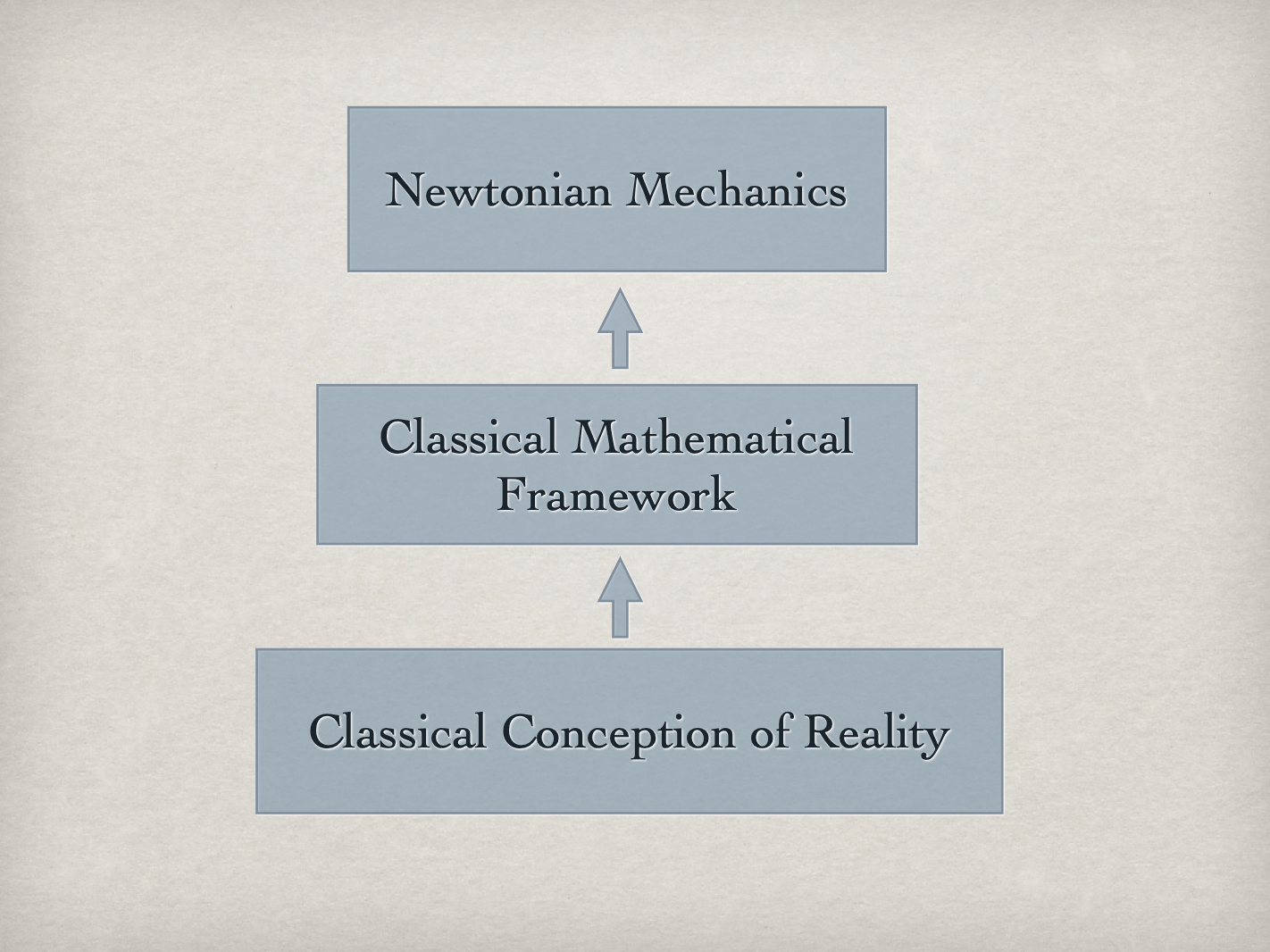
[A]: I have the mechanical conception of reality in mind.
[Q]: So you have in mind Newtonian absolute space, and time and mass, inertia, that kind of stuff?
[A]: We have to differentiate. That’s why I differentiated in the picture. When Newton first postulated this idea of a mechanical universe, it had a whole bunch of different aspects to it, the abstract notions of state, which completely represents the physical state of the system, the fact that that’s represented by a set of real numbers, the fact that that evolves according to reversible and deterministic laws in step with a universal time and that there’s a measurement process which allows complete access to that state. That’s the abstract component. Then there’s the more concrete component, in which he starts talking about absolute space and mass and inertia and gravitation - those are kind of the extra pieces. So in his work, these came all together, in a big package. Over the course of the next 250 years, this became differentiated. We realized that we can keep some of the stuff he said - the ideas of states and mappings of the state space - but we don’t necessarily need this absolute stage of space, for example. We could do without that; we could make that more fluid. We don’t need this absolute time idea, necessarily. We could do with a more flexible notion of what ‘simultaneous’ means and what time means. So when you look back retrospectively over the 250 years, you can draw a picture like this and say there’s a core idea that underlies all of classical physics and then the specific theories of classical physics are specializations of that.
The new way, which a lot of people are pursuing, is this idea of reconstruction of quantum theory. The idea is very simple: take physical principles, which you can put in the middle of this diagram, and formalize them in a simple mathematical language, and then derive the quantum formalism from those physical principles. This is the basic idea of reconstruction. Once you’ve got that, you’ll be in a much better position to go downwards and try to enclose these physical principles in some sort of ontological picture.
Going back to that picture where I had many different properties of quantum theory, if we could just pick out a couple of those and show that those are enough to derive the formalism of quantum theory, then that really helps us when we’re trying to stretch our imagination around this diverse set of phenomena that we call quantum reality. It’s much easier to look at just a couple of those and go downwards. That’s the hope.
What I’ll do is describe an outline, a derivation really, of Feynman’s rules of quantum theory. Let me talk about what they are and then I’ll explain why that’s a good idea.
Here’s a simple spacetime diagram. A particle moves from point A to point B; this is the classical picture that one would have. And Feynman’s prescription for converting this into a quantum model is the following: If you measured at A then measured at B but didn’t measure in the intervening time, you don’t actually know it went along this particular trajectory.
What you actually have to do is to consider all possible continuous trajectories that go from A to B. I’ve just drawn some of them. The rule is that you assign an amplitude, a complex number, to each of those classical trajectories, and then you speak about the total amplitude to go from A to B as being the sum of all of those amplitudes. This is the Feynman sum rule for amplitudes.
And then he has a product rule, which is the following: if you want to compute the total amplitude to go along the bold trajectory, what you can do is take the first part and multiply it by the second. If the first path has amplitude \(u_1\), you can just multiply it by \(v_1\), the amplitude for the second path. And computationally this is extremely important. It means you can break up any trajectory into lots of tiny tiny little pieces and integrate across.
And then finally the third rule links together the theoretical level of description, these amplitudes, with probabilities, those things which we actually learn about when we do experiments. The idea is the probability of detection at B, given that detection at A was found, is proportional to the amplitude, \(z\), to go from A to B, mod squared. And the proportionality is trivial—it’s fixed by normalization.
These are Feynman’s rules. They’re very interesting, because they’re actually a subset of the full von Neumann-Dirac quantum formalism, but on the other hand they’re perfectly adequate for doing calculations. They’re widely used in modern physics. The interesting thing, also, is that you already see here many of the formal features that you see in modern quantum theory that we don’t understand—the use of complex numbers, for example, the fact that you have amplitudes and probabilities, and the idea that you extract probabilities by this kind of modulus squared relationship. So, when you translate this into the state picture, you already have most of the quantum formalism.
[Q]: Causality is already there too, right?
[A]: Oh yeah. There’s a lot here. When you convert this into the state picture, the von Neumann-Dirac state picture, you get the quantum mechanics for one system, finite-dimensional. You know the transformations are linear but you don’t know they’re unitary and you don’t know about how to represent measurements yet. But, you get an awful lot. The point is you can calculate with this—you can derive Schrodinger’s equation from this. You can do a lot of stuff.
Another really interesting reason to use this, actually, is that from a strategic point of view it’s good to focus on a small subset that you know is very rich, and then expand outwards. Philosophically I like this because it gets away on the concept of state, which I have problems with, and goes to the idea of events, and process connecting events, which I think is a much more fundamental idea.
[Q]: If you don’t have a measure when you’re adding these up, basically how you weight \(z_1\), \(z_2\), \(z_3\), is this really telling us anything more than a classical theory?
[A]: When you say measure, are you talking about a measure of spaces?
[Q]: How you weight different classical trajectories.
[A]: This is the problem when you actually try to apply this to spacetime trajectories—you need a measure of the space, so you have issues there. I should have said, actually, that this whole thing can be expressed in a discrete setting, and that’s all I’ve been considering, where you have measurements with finite numbers of possible outcomes, and where the measuring of probability is not an issue.
[Q]: Are you going to view the amplitude as primitive, or does the action come into your introduction somewhere?
[A]: I’ll derive these in their abstract form, leaving how you work out the amplitude for any particular process unspecified. That is just as we find it in the quantum formalism itself. It’s up to the specific theory of particles to specify how you work that amplitude out.
You want to explain something like electron diffraction—one of the big mysteries. How would you do it? Very easily, with this Feynman picture. You just say I have a source at A that emits an electron, I have a detector here at the screen (B) that measures the electron, and I don’t know what happens in between. Classically you will commit to the idea that the particle really went along this trajectory or this trajectory.
Feynman would say no, we consider both of these trajectories. There’s an amplitude \(z_1\) for the top one, an amplitude \(z_2\) for the bottom one. The sum rule tells us that the total amplitude to go from A to B is \(z_1+z_2\), and then the probability rule takes the mod squared of that \(z\). When you do the computation, you find that the probability of detection at B, given that you found it at A, is \(p_1+p_2\), which is the classical prediction, plus an interference term. So this is where the wavelike nature of particles comes from, viewed from Feynman’s perspective. This is quite nice.
Now I’m going to show how you can derive these rules. I’m going to set up, first of all, an experimental framework. The reason for this is that Feynman talks about ‘this is what you see classically,’ and he has that as a background idea. I want to get away from that completely, and just stick with events, with measurements as the primitive notion and outcomes of measurements.
The idea is that you have a box that generates systems and when you feed it through a measurement device you get a detection at the top ring, which I’ll symbolize by 1, or a detection at the bottom ring, symbolized by 2. This is a Stern-Gerlach device. If you’re not familiar with that—it has no bearing on what I’ll actually say—it’s just a black box which, when a system comes in, generates outcome 1 or 2. And there are such things; you can just take that as a given.
One of the things we can do, which will be very important, is to merge those two detectors together. If we get this outcome, which I’ll symbolize by both 1 and 2, that just means the system passed through the device—we don’t know anything more than that. Classically, again, we would be inclined to say : ‘Really, either the system went through the top of the ring or the bottom of the ring,’ but we’re going to refrain from such speculation. We’ll just say that this is all that we see. This is just like in a double slit experiment. If we don’t have detectors which tell us the particle went this way or this way, we’ll refrain from saying anything.
The kind of setup that we’ll be interested in making predictions about will be like this, where a system—let’s say we get a 1 first, then a 1 again, then another 1—I’ll symbolize this by a sequence of measurement outcomes like this.
Or, in the second run of the experiment I get 1 first, then 2, then another 1.
I’ll be measuring the probability of these things; I’ll be doing this experiment many times, and I could do a different kind of experiment where the ring in the middle is fused now, and a typical sequence of outcomes would be like this. What I’d like to do is relate these three situations, what the probabilities would be. Classically, we’d say that’s easy. The probability of this is equal to the sum of the probabilities of the previous two. But, we know that’s not generally true.
I’m now going to define two formal ways of combining sequences together. This reflects the idea that some experiments that we do should help us determine what happens in other experiments. The idea is that somehow there’s some kind of compositionality, as a linguist would say, in these experiments.
Imagine I’ve got two sequences A and B, like this, obtained in that first experiment.
We can combine these in parallel, I will say, to generate sequence C, which I’ll symbolize with this \(\vee\). You can read this ’OR,’ if you like.
It follows straightaway from this definition that it has the symmetry that we can combine these two things in either way and we get the same sequence.
This also has the property of associativity. Imagine I have 3 sequences like this, and we combine them together.
We have to do them two at a time—we can do them like this…
…and this will be the symbolic representation of the sequence.
But you can also do it in a different way—you can think of it as A in parallel with B \(\vee\) C, and you would get this representation.
Obviously they represent the same sequence, so we could equate them, so we have associativity.
The second way of combining sequences is to do an experiment involving two measurements, and then do another experiment involving two measurements, but the last one of the first experiment coincides with the first measurement of the second experiment.
That was a bit of a mouthful—basically, I can concatenate experiments together.
I can formalize this in the following way. That is associative—if I chain 3 together, I can do them in different orders.
And finally there’s a relationship linking together these two operations, these series and parallel combination. If I take this sequence here, which is A in parallel with B,
I can chain it together with C, to generate this one here, which I symbolize like this: A in parallel with B, chained with C.
But I could also think of this in a different way: I can think of it as A in sequence with C, and at the bottom, B in sequence with C.
And I can put those in parallel, and that will generate something with looks different, but is really the same.
This is distributivity. This is actually right distributivity, and there’s a corresponding left distributivity relation.
So, this a way of composing processes that we probe experimentally, and this is the logic which underlies it.
Now, Kevin has explained already how you can go in a systematic way from a logic to a calculus. Can we do that? Can we go from this to Feynman’s rules? What we need, if we’re going to do that, is some kind of representation. As Kevin has said, you have to make a decision about what kind of representation you want. That’s not a mechanical thing—you have to make a choice. You need some input from somewhere.
The physical input essentially comes in here, to say that I’m relying on this idea of complementarity, formulated by Bohr, which I take essentially to be the idea that, to describe what’s going on in nature you need twice as many degrees of freedom as you’re able to access in a particular measurement. People talk about it in terms of wave-particle duality; when you do an experiment, you learn about one kind of aspect of a system at the expense of something else. There’s twoness there—I’m taking that to be a primitive idea.
What I’m going to do is simply postulate that we represent a sequence by a pair of real numbers \((a_1,a_2)\), and that the probability of the sequence, which I’m defining right here, is extracted from it through some well-behaved, continuous function P which we have to determine. The probability I define as the conditional probability of obtaining \(m_2\) and \(m_3\), conditional on \(m_1\). The idea is that we prepare the system in this way and say ‘What’s the probability I’ll see this and I’ll see this?’
[Q]: Why would I want this to be a conditional rather than a joint probability?
Answer: That’s a good question. So, the thing is that it’s to do with the idea that we’re considering experiments where we have a closure, so basically it’s a Markov thing. The preparation makes the past history of the system irrelevant, so we have a nice closed system, where now the outcomes that we get later on only depend on the preparation—they don’t depend on what happened before, which we don’t know in general.
[Q]: So there’s the assumption that we can actually do that.
[A]: Yes. I didn’t talk about all the details, but the idea is that measurements have this Markov property when you have atomic effects, in a technical way of speaking.
To do this representation, now, is very straightforward. It’s a mechanical process; this is briefly how it goes. If these are represented by pairs a and b, this one we say is represented by this pair, where \(\oplus\) is some binary operation to be determined.
Likewise, when we do series combinations of sequences, c is given by a \(\odot\) b, which is another operation that we need to determine.
When we do that, we go back to this picture of the logic.
That generates, on the right, these symmetries in the calculus. And as Kevin has shown so nicely in the talk before mine, these sorts of symmetries impose very strong constraints on what these operators can be, and we can solve them. I’ll step you through it very quickly so it’s not just like magic. With real numbers it’s a bit easier; with pairs you need a bit more algebra, but basically it’s the same idea.
There’s a theorem by Aczel and Hosszu that under these and other minor mathematical conditions, there’s a pair-valued function f which is invertible such that this is true. What that means is that, just as Kevin said, we can take the space of all pairs, we can act on it with a function f, and in that space this \(\oplus\) operation is simply pairwise addition.
What we can do, without loss of generality, is to go into this transformed space where a \(\oplus\) b is simply addition, like this.
That’s step 1—step 2 is that we use these distributivity conditions, and when we plug this into those, we find that a \(\oplus\) b has this bilinear multiplicative form where gamma1 through gamma8 are constants to be determined.
Finally, we use the associativity condition to constrain what these gammas can be. We find that all solutions that are possible fall into one of five classes which are either commutative or non-commutative. The first of these we recognize to be complex multiplication, so you can see where these complex numbers are arising for the first time. But there are two others, as well, which are commutative, and as you can see they’re very slight variations on complex multiplication. It’s about whether this term is present with a 0 coefficient or a +1 coefficient. And then there are two non-commutative possibilities as well.
Q Why pairs rather than triples or anything else?
[A]: Let’s save that to the end. Right now it’s a postulate that we’re dealing with a pair. It is a very interesting question to ask if we have to do that and what other things are possible.
I’ve just here shown that you can do a variable substitution and this possibility ends up looking very nice, and it’s just nice for the algebra. These are our symmetries now, and we still don’t know this a \(\odot\) b really is; it’s one of five possibilities.
We said we want to use this calculus to predict probabilities. Probability theory imposes constraints of its own.
Let’s take a sequence like this, where this is assumed to be an atomic detector—it’s a detector which isn’t a coarse graining of anything else, it’s just by itself. And that’s important. So we take this piece of sequence and represent it with pair a. We extract probability p(a) from it…
…and then we can do the same thing for this piece…
…and then of course we can do the same thing for the whole sequence, so we can say the whole sequence is a \(\odot\) b, and you can extract this probability from it.
And probability theory tells us, in this particular case, that when you use the product rule, is that these probabilities are related in a very simple way, that this probability is the product of these two probabilities.
Now we can impose this as an additional constraint, and we can take all of these 5 possibilities, solve them for p, and we end up with these solutions here, where alpha and beta are constants we have to determine. We can eliminate the ones at the bottom because the pair representation collapses to a scalar or single real value representation. When you work it through, you find that those are degenerate representations.
So we’re just left with these 3, and the argument I’ll show here is one of two ways to pare down all the way to complex multiplication. There’s another way, which is more formal.
We use the idea that, when you perform a measurement, immediately afterwards, you will get the same outcome with certainty, and that this repeatability property holds even if you put in the middle a measurement which consists of one big detector. So this behaves, as it were, like the identity. In this argument I’m actually using some input from experiment. The one way of thinking about this intuitively is that, if the measurement yields no useful information that you didn’t already know, then it needn’t disturb the system.
I won’t show you the detail of this, but when you apply this constraint, you actually restrict yourself purely to complex multiplication here, and you fix the value of alpha to be 2, so you end up with this relationship here.
This completes the derivation of Feynman’s rules. In the notation I’ve got, you end up with these 3 rules: the sum rule, the product rule, and the probability rule. Why complex numbers are so natural in quantum theory is evident here. It follows from those symmetries and those constraints.
Just a quick overview of the argument—very quickly—we’ve used symmetries in the logic of process, and then we’ve imposed constraints from probability theory, and we finally use another argument here to get down here.
So, as I said, the Feynman rules don’t exhaust the content of the quantum formalism—you might ask ‘Well, what about the rest?’ It can be completed. We’ve always been considering one system, but if you consider two systems, we can write down similar symmetry relationships about them which must be satisfied, and seek representations of those. When we do that, we find that we get what we know of as the tensor product rule from quantum theory. And then we want to introduce the concept of state which can be done using no new ideas, just what we have already. When we do that, we find immediately that measurements are represented by Hermitian operators.
We can ask about evolution of states; we find that we need some extra idea to get unitary evolution, interestingly enough. There are a couple of possibilities so far of how you can do that. One is to say that it’s not possible to instantaneously signal by performing a measurement on this system. Interestingly, you do need something more. Obviously, then, if you really want to apply this to a system, you need something like the temporal evolution operator, which requires more ideas, more input.
Just a summary of ‘Where do Feynman’s rules of quantum theory come from?’; it’s very simple. Feynman’s rules are a pair-valued representation of a logic of process, which is consistent with probability theory. That, I think, encapsulates what’s going on.
And, an immediate implication—there are many implications; I’ll just focus on one that’s very interesting—is nowhere here have I talked explicitly about space and nearness in space and metrics of space, or dimensionality of space. It’s appeared in the most minimal sense, that I know that there are events that happened, so somehow they’re distinguishable from one another. So they must have occurred at different spatial points, let’s say, but the idea of space has hardly entered the derivation. And certainly I haven’t talked about matter or fields, I haven’t talked about particles, mass, momentum, energy. Time has entered only in the minimal sense of temporal ordering. I need an idea of ordering - this happens, then that, then that. I also haven’t used the idea of nearness in time. So I don’t have a metric over time. There’s an awful lot that’s not here. What this shows, I think, is that the quantum formalism, at its heart, is a self-standing theoretical structure. It doesn’t need to lean on classical notions to stand upright, and it’s very solidly founded in this idea of this process logic. Its status is comparable to the status of probability theory.
Very briefly, I’ll just mention one interesting connection that you make when you do this to real number systems, or to the number systems in mathematics.
You’ve got the algebras of real numbers and it has these symmetries, plus some more. What you can do is say ‘Is it a representation of a logic? Is it a representation of something more fundamental?’
You can do that, of course; you can abstract from the right to the left, where A B and C now are abstract numbers, abstract mathematical entities. They satisfy these same symmetries as on the left, obviously. What we can then do is ask ‘Can we generalize the real number system?’ which is something that, as a mathematician, you might want to do. You say ‘I’m tired of dealing with these single numbers, I want pairs of numbers, or tuples, or matrices, or something more general. Can I do that?’ You could say my desideratum is these symmetries should be satisfied as far as possible. That’s something that you might want.
What you can do is seek a general representation of this, where the little a b and c are just abstract mathematical entities which we haven’t specified yet.
You can just check that it works; you can ask for a real-valued representation of this and, then following everything that Kevin said, it follows from this associativity condition that this holds. All you need is continuity at a point, by the way, so the additional mathematical assumptions you need are minimal.
This is automatically satisfied, interestingly enough. You get that for free.
You can either use the middle condition, or I’ve chosen to use these two on the bottom. If you substitute this into these two you find, without loss of generality, you get this product.
And in this case, you get associativity on the left here for free. You can kind of reconstruct the real number system from these symmetries.
But of course now that we’ve abstracted from the real number system you can ask ‘What about pair-valued representations?’ Then, you see, we’re back to the derivation of Feynman’s rules. These are the very same symmetries that I’ve got in the process logic and, as you can see, they’re already there in the number systems of mathematics, which is a striking thing that these two are connected together at such a deep level.
Exactly the same mathematics applies—this is just recapitulating what I already said. And interestingly, notice that you have a whole bunch of possibilities here, so you need to impose additional mathematical desiderata if you want to pick out complex multiplication. You can do that by requiring that every non-zero element has a multiplicative inverse. If you want to get rid of the bottom two, you can say ‘I don’t like non-commutativity in my multiplication,’ and then you end up with these three. I didn’t know this until after I did this work, but the mathematicians already knew about these 150 years ago. They call these dual numbers and these double numbers, confusingly enough. So they actually have names for these. And they’ve been independently rediscovered a dozen times, which is incredible. There’s like ten different names for these things. It’s very interesting.
We can see this wonderful parallel between quantum theory and these number systems. Basically, they share these common symmetries which come from very different sources, and in this case we needed this extra little piece to get down to the complex structure. Over in the mathematical domain you don’t have that kind of constraint so you impose some other kind of constraint that seems natural to you, and you get complex structure. In other words, there’s a sort of deep common core to both of these, which gives a very deep answer to the question ‘Why is quantum theory complex?’ It’s because there’s a huge common ground here; these are the symmetries which, by and large, characterize complex numbers in mathematics.
[Q]: But you said that the reals also obey these. So why complex rather than real?
[A]: Right, can I talk about that in a minute?
Finally, now, this is the picture we have. Our postulate box is filled with this, what we call the pair postulate, that has this twin idea that measurement outcomes are probabilistic; we just take that as a given. Of course, the theory could say ’No, the probabilities are actually always 0 and 1,’ so we don’t actually them to be other than 0 and 1, but the formalism tells us it’s possible. And we have this idea of complementarity, formalized in this very precise way. There’s nothing vague or quixotical about it, we just have a pair of real numbers.
The question is ‘Do I have anything to say about a quantum conception of reality?’ It’s difficult. The next job is to go downwards. What can we say about this? Quite a few things—I’ll just say one thing, and then I’ll close.
Essentially, in the classical picture of measurement, it’s assumed we have this very direct access to reality; our measurement outcomes are deterministic, and we have complete accessibility of the degrees of freedom and the state of a system. So we have this complete, unfettered access to what’s there. What it means, as was mentioned yesterday, is that every agent has this kind of God’s eye view of reality—every agent has the same God’s eye view of reality, so there’s actually no differentiation in the knowledge that they could have about reality, in principle. In reality they’ll have different capacities because not everyone can afford an electron microscope, but in principle they have the same access.
Now what we have in the quantum picture is that that access is fundamentally limited. It’s limited in two ways. Outcomes are probabilistic, meaning that when you make a measurement, you get a certain amount of information. You must perform many different measurements, and you actually must perform many separately prepared copies of the system. That’s because when you make measurements, if they’re to be repeatable, you end up disturbing the state radically, every time. Also, because of complementarity, when you make a given measurement on a system, you only see half of the degrees of freedom in the state of the system. More precisely, if it’s a pure state and you do a repeatable measurement, you only see half the degrees of freedom in the state of the system. So there’re two distinctive ways in which quantum theory restricts what we can learn. We have this idea that in principle, now, agents will have different knowledge about the state of the system, and that’s because of their history. Their history matters. There’s always this gap between what an agent can know and what the state really is.
Thank you for your attention—this is a reference which describes the work.
[Q]: The language you used in the last 2 minutes of your presentation indicates that you have an image of quantum reality that the wavefunction represents incomplete knowledge of a hidden state, and the hidden state gets disturbed when measurements are made. You said almost precisely that. So what are your feelings on the Bell inequality violations? Are you comfortable with the necessity of these hidden states being not locally attributable to systems? Are you working with the imagery of nonlocal hidden variables?
[A]: I’m not working with the idea of hidden variables, no.
[Q]: So what distinguishes your view from a hidden variable view?
[A]: The common view is that there are hidden variables which would determine, theoretically, which outcome you’ll get, but those are inaccessible, so you end up with a stochastic outcome. That’s certainly not what I mean. I’m not saying there’s a deterministic underpinning of the probabilistic nature of outcomes. Let me go back to the thing you mentioned with the Bell inequality violation. One of the implications that I draw from this, correctly or incorrectly, is that space as a stage where everything happens isn’t really fundamental at all. The quantum formalism is really more primitive. And, if you take that view, then you would in general not expect there to be anything fundamental about locality. So in general, the surprise is that so much of our experience is local in its nature.
[Q]: I wanted to come in precisely at that point. I’m just wondering whether you aren’t actually wiping away something that you shouldn’t. You talked about detectors, then you said you just wanted to know that something had happened there. Now, detectors, if I’m not mistaken, are always devices in a very very special state. They’re metastable states which is quite a complex thing. It’s essentially a lattice of some form or another of a metastable state. So I’m just wondering whether that isn’t a little bit, when you say ‘All of this is quite independent of space and time,’ I’m just a little bit skeptical about it.
[A]: That’s why I said there’s a question mark against that. Let me try to deal with it in the following way: I’m taking what’s known as the operational view to things, where we say that all that we know is we set up measurements and we get outcomes in certain sequences, and that’s the primitive input that we get when we do an experiment. The advantage of this approach gives you a firm bedrock on which to then build up something like the full quantum formalism. The disadvantage is that you then have to swallow these primitive notions of measurement and detectors and events, outcomes of those datectors. So that’s obviously a problem, and I’m not happy with it either, but it seems that that operational view does force you that way. How I deal with that metaphysically is a different issue, and I think that’s the question of ‘What conception of reality does this suggest?’ I’m certainly of the opinion, and have been for some time, that we need to embrace something more like an Aristotelean metaphysics, where there is a process of actualization that happens, and that that isn’t—we normally think of it as, when we do a measurement, an outcome is obtained, but I would view the idea that in nature by itself there are these processes of actualization that happen in the normal course of things, what you would normally call objective reduction, let’s say, in the literature. All the time there are these actualizations actually happening as part of the natural dynamics. So, from that point of view, this idea of unitary evolution, where there’s no actualization, and measurement where there’s an actualization, are two polar idealizations about how we deal with nature. But actually, what’s going on right now are both processes, and maybe something in between, and we’re kind of describing it in this very simplistic, idealized way. So then when you bring actualization into nature itself, then that obviously leads you in a completely different direction. What I’m saying is that the operational way of thinking is a way to get the formalism. Then you still can interpret it in a different way.
[Q]: More of a comment than a question. When you were talking about the extent to which you got quantum mechanics out, you expressed some surprise that you need something more to get unitarity. This doesn’t seem surprising to me, because you don’t have any dynamics. You’re not using the action in your path integral. Those \(z\)’s are arbitrary. So for arbitrary dynamics there’s no particular reason why you would expect it to have energy conservation, unitarity, all these things that have to do traditionally with dynamics. So what you end up with is a generalized framework which, I suppose, if you stick in an appropriate action and you’re deriving \(z\)’s from a particular kind of action, then you get much of the rest of what you expect of quantum mechanics.
[A]: But you actually need very little. For example, the axiom of no signaling is enough to get unitarity from this approach. So I just need to postulate that if you and I share an entangled state, I can’t make a measurement on my side, get an outcome, and you can thereby figure out that I’ve signaled to you.
[Q]: Then this is for nonrelativistic theories?
[A]: No. If you take the Feynman rules and you translate them, you introduce the concept of state, you get the finite-dimensional von Neumann-Dirac formalism with evolution with evolution represented by linear transformations. You end up with matrices which you know are linear.
[Q]: But you said you didn’t have any space. So I don’t know what…
[A]: You don’t need space to get unitarity.
[Q]: No, but you had a no signaling condition. Isn’t that typically what you mean by no signaling?
[A]: Well, you need the notion of independent systems. You don’t need space. You need the idea that I have a system, and you have a system, and the idea that they’re statistically independent. You don’t need the notion of space, necessarily. That could be a derived secondary notion. You could say we’re far apart if I can’t signal you. You could turn the logic upside down.
[Q]: I could see why you want to focus on quantum mechanics, but I was just thinking, this might be an interesting way to map out alternatives if something goes wrong, right? So you’ve got this kind of morphism perspective on logical principles and numbers, and you could get an ordered diagram of ways in which symmetries could get knocked out by nature, and you could get new theories, right? Of course, in logic, when you knock out one axiom, that doesn’t mean you just knock it out, right? You could put in weaker ones of the sort that have been looked at in nonstandard algebraic logic and get different kinds of theories for those, right? You could sort of map out the future of physics if things go wrong.
[A]: One of the big motivations to do this kind of thing is precisely that: to help guide the future development and to be able to say, when we say quantum theory, it means a lot of stuff. It means the von Neumann-Dirac formalism, which has lots of different pieces, and then there’s the commutation relationships and so on, but that’s an undifferentiated blob. It would be nice to sort of separate it out and say ‘Look, there’s some part of this which is really really basic, and there’s some part of it which seems less basic,’ and then all the way up to a certain point where you say ‘Actually, here I’m putting in this notion of energy, which comes from classical physics, to get temporal evolution’ or something like that. And maybe I’m not happy with that. So this bears on the discussion yesterday: could the laws of physics be mutable? When you do this kind of reconstruction, you can stand back and say ‘Ah, well, this logic of process doesn’t look very mutable.’ Representation doesn’t look very mutable because 2 can either be 1 or 3 or 4 but it can’t continuously change, so it doesn’t look like there’s much flexibility there. So at what point in the chain could I have some continuous parameters that could change gracefully without breaking the structure? It’s not that obvious to me, having looked at it briefly. I hadn’t really thought about this before yesterday, actually, about the mutability idea, but it seems that hbar is the only thing which comes in way at the end; it comes in through the temporal evolution law, which is the last thing on the slide that I had. It doesn’t seem that you can gracefully change that structure at the beginning, but what you said, I hadn’t thought about weakening those axioms for the logic of process.
[Q]: Like distributivity, for some reason.
[A]: Yeah, but the question is ‘Could you do it,’ and maybe we should talk about that, how it could be done.
[Q]: About the representations in real numbers and pairs of real numbers: are there other representations?
[A]: Let me talk about that. I put that off during the talk. The question is, can you do a real number representation? The answer is yes, everything works, the derivation works…
[Q]: I’m asking whether there are other discrete representations, like some other field or something.
[A]: So you’re taking a mathematical object that’s no even an n-tuple, you mean?
[Q]: Not a continuous one, but a discrete one.
[A]: Like a rational number pair?
[Q]: For example. Or even more discrete, like a finite set.
[A]: I disavow you to look into this. The mathematics gets quite hairy once you don’t have continuity. So basically these functional equations turn out that if you have continuity at a point and deal with real numbers, everything is nice. As soon as you lose that you’re not dealing with real numbers; you go to rational numbers. Then you need additional properties that replace continuity, like cancellativity.
[Q]: Well if you only have this associativity, it seems that there’s no continuity requirement, on the surface.
[A]: Yeah, and I have a lot of hope that you can do this without assuming real numbers, and my hope is based on the fact that Janos Aczel, who’s this mathematician behind these theorems that we’re quoting, he has indeed shown that the associativity equation can be solved for rational numbers, but you need something else. Some cancellativity property or monotonicity property. So you need extra things. And from a physics point of view, the question is what would justify that, those mathematical assumptions? I’m happy to deal with real numbers and continuity because, I guess, I’m more familiar with it. But yes, these are absolutely great questions and the question then is can we stretch the mathematics so we can go beyond real numbers?
[Q]: This may be a naive comment/question, but, to look at the history of how quantum mechanics came about, it was really from all the experiments that came up and challenged people to think in different ways, and so all sorts of views came up, and they came up with this formalism, but it seems to me that basically, you can invent a set of rules that is compatible with what people have found in other ways with quantum mechanics. So you can perhaps play this game in a more general way and say ‘If I change my rules, what kind of other implementations of natural systems can I come up with?’ And maybe that way you can think of ‘Why isn’t nature choosing this particular set of rules?’ and not other sets of rules.
[A]: But are you thinking about the logic being changed?
[Q]: Yes. If there were no experiments, in principle, people could have invented quantum mechanics from just hitting on the right set of rules. That’s what I mean.
[A]: What I suppose I’m saying is I can’t see any reason why this couldn’t have been done 150 years ago. The logic of process is so obvious. It’s actually just restraining yourself from making metaphysical speculations about what’s going on when you haven’t measured. Just obeying that dictum gives you the logic. The key point is why do we choose a pair valued representation.
[Q]: Right, but that begs the question which, I don’t know if there is an answer to it or not: why is nature choosing this particular set, and not another set?
[A]: You mean this particular logic?
[Q]: Right.
[A]: I don’t think nature’s actually choosing that. That’s just a language for describing what we see.
[Q]: Well, that’s saying the same thing backwards.
[A]: Is it?
[Q]: I think you’re asking why is nature choosing the pair-valued representation.
[A]: That’s a different question. I think I’ve been asked the question about where does the logic of process come from. It’s two questions. My view is that that logic, I can’t see that it admits any variation. I think that’s an absolutely minimal statement. It’s a bit like the boolean logic of propositions; it has the same status. It’s very basic. I can’t see any way of changing that. But maybe I’m wrong, and it’ll be great to know if there is a way of changing it. The question about the pair-valued representation, let me finally address that properly. If you take a real number, the same derivation goes through, and what you get is quantum mechanics restricted to real numbers. The derivation I’ve got right now can’t say why that’s wrong.
[Q]: Or triples?
[A]: Okay, so let me go to that. In the case of real or complex quantum mechanics, it seems like we need some additional idea to say why complex quantum mechanics holds. I’m unsettled on what that further idea might be.
[Q]: What about unitarity? Do you still get unitarity?
[A]: Yeah, you get the equivalent of unitarity, basically, you get orthogonal transformations. You get unitarity restricted to the real numbers. The real vs. complex quantum mechanics, one idea is there’s this notion of what’s called local tomography. The idea is, imagine I have a bipartite state, or two different bipartite states that I give to you and you and a friend, by making measurements on each separate system, figure out that these are different states? Can you distinguish between them? Can you distinguish between all possible bipartite states by these local operations? If you can, that’s called local tomography. Now, this comes back to this promise that’s made in the mechanical conception of reality. Is reality so constituted that it’s nice to us, that we can figure out what’s going on by doing local operations alone? If we can, that’s the property of local tomography. That singles out complex quantum mechanics, and that eliminates real quantum mechanics.
[Q]: How about triples?
[A]: Okay, so now the triples. The actual question is ‘Why not triples? Why not arbitrary n-tuples?’ Simple answer—I don’t know for sure. But, the mathematicians have very powerful theorems which say that if you try to create number systems satisfying the symmetries I described, then in fact you have very few possibilities. There’s a general theorem that says—you need more than just the symmetries I’ve described—you have real, complex, quaternion and octonions. So 1, 2, 4 and 8 are the only possibilities. And you find that the quaternion case has non-commutative multiplication, which is ruled out at some point in the derivation, and the octonions are not associative in multiplication. That’s certainly ruled out by the logic of calculus straight away. So if—now this is a big ‘if’—it’s possible to somehow take what the mathematicians have done and translate it over into this framework, then I hope we could eliminate all but real and complex, and we’ll be forced, by local tomography to complex. That’s the program. That’s the hope. But the mathematicians use language and assumptions that aren’t natural to me at the moment. So it’s a question of ‘Can we translate those ideas?’
[Q]: It’s kind of a marginal comment, but maybe I think it’s worth making because people missed the point. In some sense, the actual classical picture of almost all classical physicists is of an ontology of continuous, flexible substances. Now, many physicists act like the transition from discrete numbers of degrees of freedom to an infinite number to get a genuine continuum is fairly trivial or straightforward. There’s no worker in rigorous continuum mechanics who believes that and thinks that all those changes of summation into integration are horrible moves to make. When you do it properly in a continuum mechanics framework, then it’s often the case that many of your local assumptions break down. So we’ll have, over volumes, well-defined momenta and so forth, but they do not always induce those properties on a local level. There’s always the possibility that you need to think about a formulation of quantum mechanics more from a global perspective.
[A]: I think until the advent of quantum information and computing, there was a great emphasis put on the infinite-dimensional quantum formalism, and actually saying that’s the thing we should try to understand. But I think that quantum information and computing shows that so much comes from looking at finite-dimensional systems. The reconstructive efforts, most of them, are trying to say ‘Actually, the finite-dimensional formalism is enough.’ There are a few other points. Secondly, if you take this operational point of view, the idea of a non-denumerably infinite number of outcomes is a very strange one, because operationally we can’t ever get that. We only have a finite number of detectors. So that, from an operational point of view, pushes you to the finite-dimensional formalism very naturally. And then finally, I think, my own view is that the finite-dimensional formalism is really the formalism. The infinite-dimensional case is really an approximation, a convenient way of calculating with very large numbers of detectors, but finitely many of them. Certainly, clues from black hole thermodynamics and so on also seem to be pointing in the direction that this idea of a continuum of space is a kind of fiction, and in fact that there are actually finitely many degrees of freedom which are actually needed.